
探索性數據分析
EDA的提出
1977年,美國統計學家John W. Tukey出版了《探索性數據分析》一書,引起了統計學界的關注。該書指出了統計建模應該結合數據的真實分布情況,對數據進行分析,而不應該從理論分布假定出發去構建模型。EDA重新提出了描述統計在數據分析中的重要性,它為統計學指明了新的發展方向——和數據相結合。
EDA的定義

探索性數據分析是對調查、觀測所得到的一些初步的雜亂無章的數據,在盡量少的先驗假定下進行處理,通過作圖、制表等形式和方程擬合、計算某些特征量等手段,探索數據的結構和規律的一種數據分析方法。
EDA的主要特點
研究從原始數據入手,完全以實際數據為依據
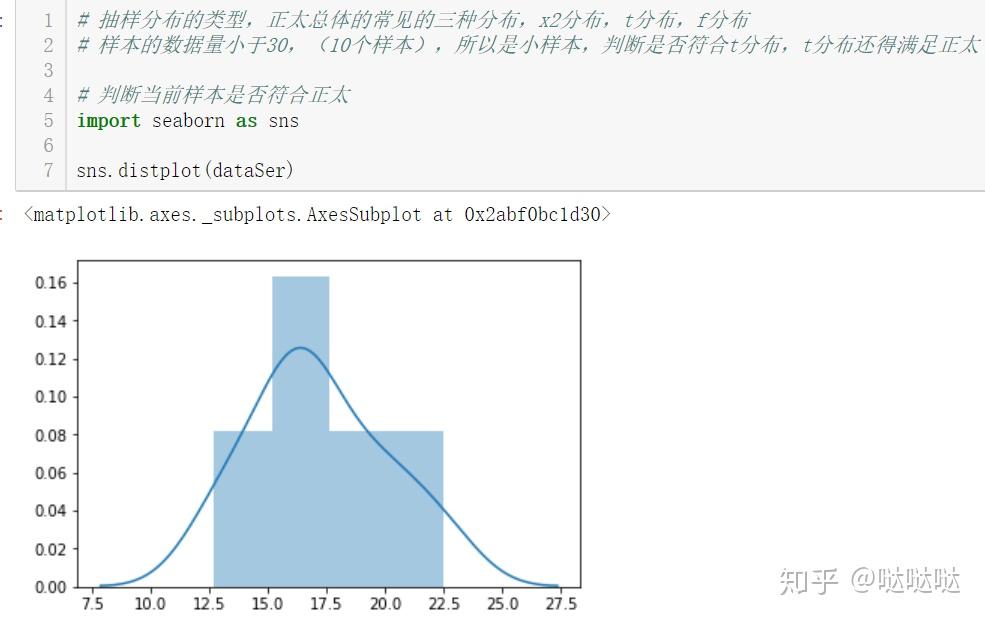
傳統的統計分析方法通常是先假定數據服從某種分布,然后用適應這種分布的模型進行分析和預測。但實際上,多數數據(尤其是實驗數據)并不能保證滿足假定的理論分布。因此,傳統方法的統計結果常常并不令人滿意,使用上受到很大的局限。
分析方法從實際出發,不以某種理論為依據
傳統的統計分析方法是以概率論為理論基礎探索性數據分析 pdf,對各種參數的估計、檢驗和預測給出具有一定精度的度量方法和度量值。而EDA在探索數據內在的數量特征、數量關系和數量變化時,什么方法可以達到這一目的就采用什么方法,靈活對待,靈活處理。方法的選擇完全取決于數據的特點和研究的目的。

單變量分析
頻率和眾數:針對于無序的分類的變量
百分位數:針對于有序的或連續的變量

位置度量:均值和中位數
散布度量:方差、標準差、偏度、峰度、四分位數極差
偏度和峰度

偏度的計算公式:
偏度是刻畫數據對稱性的指標。關于均值對稱的數據其偏度為0,呈現右偏的數據偏度大于0,呈現左偏的數據偏度小于0。
峰度的計算公式:
峰度是刻畫分布狀態的陡緩程度的指標。峰度等于0,分布呈正態,峰度大于0,分布呈尖峰狀態,峰度小于0探索性數據分析 pdf,分布呈平峰狀態。